Correlation – Meaning, Definition, Importance, Significance, Types, Properties Degrees & Methods

DrGaurav
coefficients of correlation meaning definitions, significance importance, and characteristics nature types, methods, properties, degrees, karl pearson's coefficient of correlation, spearman's rank correlation, and scatter diagram method

In this article, we will discuss the meaning, concepts, definitions, needs, significance, importance, properties, types, and methods of correlation coefficients. types and methods of correlation – Scatter Diagram Karl Pearson’s co-efficient of correlation, Spearman’s Rank co-efficient Correlation

Meaning, concept, definitions, needs, significance, importance, properties, types and methods of correlation

Meaning of Correlation:

The following is the meaning and concept  of correlation:

Meaning: Correlation refers to a statistical measure that describes the relationship between two variables. It is a measure of the strength and direction of the association between two variables. Correlation can range from -1 to 1, with a value of 0 indicating no correlation.

A positive correlation means that as one variable increases, the other variable also tends to increase. Conversely, a negative correlation means that as one variable increases, the other variable tends to decrease.

Correlation does not imply causation, meaning that just because two variables are correlated, it does not necessarily mean that one causes the other. There may be other factors or variables that affect the relationship between the two variables. Therefore, it is important to be cautious when interpreting correlations and to consider other factors that may be influencing the relationship.

Definitions of Correlation:

The following are some definitions of Correlation:

According to L.R. Connor, “If two or more quantities vary in sympathy so that movements in one tend to be accompanied by corresponding movements in others, then they are said to be correlated.”

In the words of Croxton and Cowden, “When the relationship is of a quantitative nature, the appropriate statistical tool for discovering and measuring the relationship and expressing it in a brief formula is known as correlation.”

According to A.M. Tuttle, “Correlation is an analysis of covariation between two or more variables.”

Significance of the Study of Correlation:

The following are some significant or importance of correlation analysis

1. Correlation measures the strength of relationship between two or more variables. For example, the relationship between income and consumption expenditure, price and quantity demanded etc.

2. When the nature of relationship between variables is known, it is easy to predict the value of one variable when the other variable is known.

3. It helps in understanding the behaviour of various economic variables like, demand, supply, GDP, interest, money supply, inflation, income and expenditure and so on.

4. In business firms, it helps in making decisions on cost, price, sales, advertisement etc.

Need and Importance for Correlation:

The followings are the need and importance of the correlation

Correlation gives meaning to a construct. Correlational analysis is essential for basic psycho-educational research. Indeed most of the basic and applied psychological research is correlational in nature.

Correlational analysis is required for:

(i) Finding characteristics of psychological and educational tests (reliability, validity, item analysis, etc.).

(ii) Testing whether certain data is consistent with the hypothesis.

(iii) Predicting one variable based on the knowledge of the other(s).

(iv) Building psychological and educational models and theories.

(v) Grouping variables/measures for parsimonious interpretation of data.

(vi) Carrying multivariate statistical tests (Hoteling’s T2; MANOVA, MANCOVA, Discriminant analysis, Factor Analysis).

(vii) Isolating influence of variables.

Co-efficient of Correlation:

To measure the degree of association or relationship between two variables quantitatively, an index of relationship is used and is termed a co-efficient of correlation.

The coefficient of correlation is a numerical index that tells us to what extent the two variables are related and to what extent the variations in one variable change with the variations in the other. The coefficient of correlation is always symbolized either by r or ρ (Rho).

The notion ‘r’ is known as the product-moment correlation coefficient or Karl Pearson’s Coefficient of Correlation. The symbol ‘ρ’ (Rho) is known as the Rank Difference Correlation coefficient or spearman’s Rank Correlation Coefficient.

The size of ‘r‘ indicates the amount (or degree or extent) of correlation between two variables. If the correlation is positive the value of ‘r‘ is + ve and if the correlation is negative the value of V is negative. Thus, the signs of the coefficient indicate the kind of relationship. The value of V varies from +1 to -1.

Correlation can vary in between perfect positive correlation and perfect negative correlation. The top of the scale will indicate perfect positive correlation and it will begin from +1 and then it will pass through zero, indicating the entire absence of correlation.

The bottom of the scale will end at -1 and it will indicate perfect negative correlation. Thus numerical measurement of the correlation is provided by the scale which runs from +1 to -1.

[NB—The coefficient of correlation is a number and not a percentage. It is generally rounded up to two decimal places].

Types of Correlation

The following are the various types of correlation based on the direction of change, number of variables, the ratio of variation

Types of Correlation coefficient of correlation methods techniques

Types of Correlation: Based on the direction of change:

Positive correlation refers to a relationship between two variables where an increase in one variable is associated with an increase in the other variable. For example, there may be a positive correlation between the amount of exercise and physical fitness, as individuals who exercise more are likely to be more physically fit. A positive correlation coefficient is represented by a value between 0 and +1.

Negative correlation refers to a relationship between two variables where an increase in one variable is associated with a decrease in the other variable. For example, there may be a negative correlation between the amount of sugar consumed and dental health, as individuals who consume more sugar are likely to have worse dental health. A negative correlation coefficient is represented by a value between 0 and -1.

Types of Correlation: Based on a number of variables:

Simple correlation refers to the relationship between two variables. For example, the relationship between height and weight can be studied using simple correlation.

Partial correlation refers to the relationship between two variables while controlling for the effects of one or more additional variables. For example, the relationship between height and weight can be studied using partial correlation while controlling for the effects of age.

Multiple correlation refers to the relationship between a dependent variable and two or more independent variables. For example, the relationship between academic performance (dependent variable) and study time, sleep time, and diet (independent variables) can be studied using multiple correlations.

Types of Correlation: Based on the ratio of variation in the variables:

Linear correlation refers to a relationship between two variables that can be approximated by a straight line. For example, the relationship between temperature and ice cream sales is often linear.

Non-linear correlation refers to a relationship between two variables that cannot be approximated by a straight line. For example, the relationship between age and memory may be non-linear, as memory may improve in early adulthood, decline in middle age, and then decline more rapidly in old age. Non-linear relationships can take different forms, such as quadratic, exponential, logarithmic, or sinusoidal.

Methods of Correlation – Scatter Diagram, Pearson’s Coefficient of correlation, Spearman’s Rank Correlation 

The following are some methods of correlation – Scatter Diagram, Pearson’s Co-efficient of Correlation, and Spearman’s Rank Correlation Tests. Methods & properties of coefficient of correlation

Correlation is a statistical technique that measures the strength and direction of the relationship between two variables. There are several methods of correlation, including a scatter diagram, Pearson’s correlation coefficient, and Spearman’s correlation coefficient.

  1. Scatter Diagram: A scatter diagram is a graphical representation of the relationship between two variables. It involves plotting the values of one variable on the horizontal axis and the values of the other variable on the vertical axis. The resulting pattern of points on the graph indicates the strength and direction of the relationship between the two variables.
  2. Pearson’s Correlation Coefficient: Pearson’s correlation coefficient (also called Pearson’s r) is a measure of the linear relationship between two variables. It ranges from -1 to +1, with values closer to +1 indicating a strong positive relationship and values closer to -1 indicating a strong negative relationship. A value of 0 indicates no relationship.
  3. Spearman’s Correlation Coefficient: Spearman’s correlation coefficient (also called Spearman’s rho) is a non-parametric measure of the strength and direction of the relationship between two variables. It is based on the ranks of the values rather than the actual values themselves. Spearman’s rho ranges from -1 to +1, with values closer to +1 indicating a strong positive relationship and values closer to -1 indicating a strong negative relationship. A value of 0 indicates no relationship.

Both Pearson’s and Spearman’s correlation coefficients have their advantages and disadvantages, and the choice of which to use depends on the nature of the data and the research question. Pearson’s correlation coefficient is suitable for normally distributed data that have a linear relationship, while Spearman’s correlation coefficient is more appropriate for non-linear relationships or when the data is not normally distributed. Correlation Meaning Definitions Types Methods

Methods & properties of coefficient of correlation

1. Scatter Diagram Method of Correlation

A simple and attractive method of measuring correlation by diagrammatically representing bivariate distribution for determination of the nature of the correlation between the variables is known as Scatter Diagram Method. This method gives a visual idea to the investigator/analyst regarding the nature of the association between the two variables. It is the simplest method of studying the relationship between two variables as there is no need to calculate any numerical value. 

The scatter diagram is a graphical method used to display the relationship between two variables. It is a simple and effective way to identify patterns and trends in data.

To create a scatter diagram, you need to plot the values of one variable on the horizontal axis and the values of the other variable on the vertical axis. Each point on the graph represents a pair of values for the two variables. The pattern of points on the graph can provide valuable insights into the relationship between the two variables. Correlation Meaning Definitions Types Methods

If the points on the scatter diagram form a roughly straight line, then the relationship between the two variables is said to be linear. A line of best fit can be drawn through the points to summarize the relationship. If the points on the scatter diagram do not form a straight line, then the relationship between the two variables may be non-linear, and other methods of correlation may be more appropriate.

Scatter diagrams are commonly used in fields such as economics, finance, and environmental studies to identify relationships between variables. They are also useful for identifying outliers or unusual data points that may be affecting the relationship between the variables.

In summary, the scatter diagram is a simple yet powerful method of correlation that can help identify patterns and trends in data. It is a valuable tool for analyzing relationships between variables and for identifying outliers or unusual data points. Correlation Meaning Definitions Types Methods

Advantages of Scatter Plot

The scatter plot helps in describing the association by analyzing the following factors.

  • Direction
  • Curvature
  • Variation
  • Outliers

From a scatter plot, we can understand whether the correlation is positive or negative, linear or not, whether the data is tightly clustered, and if there is the presence or absence of any outliers.

With the scatter of dots in the graph, we can form an idea of the nature of the relationship.

  • If all of the points are on a straight line, the correlation is perfect and is referred to as unity.
  • The correlation is weak if the scatter points are widely dispersed around the line.
  • If the scatter points are close to or on a line, the correlation is linear or strong.
Scatter Plots

Various degrees of correlation between two variables can be shown with the help of scatter diagrams as given below:

i. Perfect Positive Correlation:

In a perfect positive correlation, all the dots lie in a straight line and are upward-sloping. The correlation coefficient (r) would be equal to +1, when the correlation is perfectly positive.

ii. Perfect Negative Correlation:

In a perfect negative correlation, the dots lie on the same line and are downward-sloping. The correlation coefficient (r) would be equal to -1 when the correlation is perfectly negative.

iii. High Degree of Positive Correlation:

When the points come closer to a straight line and are moving from bottom left to top right, there is said to be a high degree of positive correlation. The value of the correlation coefficient (r) would lie between + 0.7 and + 1.

iv. High Degree of Negative Correlation:

When the points come closer to a straight line and are moving from top left to bottom right, there is said to be a high degree of negative correlation. The value of the correlation coefficient (r) would lie between – 0.7 and – 1.

v. Low Degree of Positive Correlation:

In this case, the points are widely scattered but are rising from the lower left to the upper right. The value of the correlation coefficient (r) would be close to 0 but positive.

vi. Low Degree of Negative Correlation:

In this case, the points are widely scattered but are falling from the upper left to the lower right. The value of the correlation coefficient (r) would be close to 0 but negative.

vii. No Correlation:

When there is no relationship between variables, the points would be scattered all over and would not move in any direction. The value of the correlation coefficient (r) would be equal to zero when there is no relationship between variables. Correlation Meaning Definitions Types Methods

How to draw a Scatter Diagram?

The two steps required to draw a Scatter Diagram or Dot Diagram are as follows:

  1. Plot the values of the given variables (say X and Y) along the X-axis and Y-axis, respectively.
  2. Show these plotted values on the graph by dots. Each of these dots represents a pair of values.

Interpretation of Scatter Diagram

After observing the pattern of dots, one can know the presence or absence of correlation and its type. Besides, it also gives an idea of the nature and intensity of the relationship between the two variables. 

The scatter diagram can be interpreted in the following ways:

1. Perfect Positive Correlation:

If the points of the scatter diagram fall on a straight line and have a positive(upward) slope, then the correlation is said to be perfectly positive; i.e., r = +1.

Perfect Positive Correlation

2. Perfect Negative Correlation:

If the points of the scatter diagram fall on a straight line and have a negative(downward) slope, then the correlation is said to be perfectly negative; i.e., r = -1.

Perfect Negative Correlation

3. Positive Correlation:

When the points of the scatter diagram cluster around a straight line (upward slope from left to right), then the correlation is said to be positive.

Positive Correlation

4. Negative Correlation:

When the points of the scatter diagram cluster around a straight line (downward/negative slope), then the correlation is said to be negative.

Negative Correlation

5. No Correlation:

When the points of the scatter diagram are scattered haphazardly, then there is zero or no correlation. 

No Correlation

How to interpret a Scatter Diagram?

While interpreting a scatter diagram, the given below points should be taken into consideration:

  • Dense or Scattered Points: If the plotted points are close to each other, then the analyst can expect a high degree of correlation between the two variables. However, if the plotted points are widely scattered, then the analyst can expect a poor correlation between the variables.
  • Trend or No Trend: If the points plotted on the scatter diagram shows any trend either upward or downward, then it can be said that the variables are correlated. However, if the plotted points do not show any trend, then it can be said that the variables are uncorrelated.
  • Upward or Downward Trend: If the plotted points show an upward trend rising from the lower left-hand corner of the graph and goes upward to the upper right-hand corner, then the correlation is positive. It means that the two variables move in the same direction. However, if the plotted points show a downward trend from the upper left-hand corner of the graph to the lower right-hand corner, then the correlation is negative. It means that the two variables move in the opposite direction.
  • Perfect Correlation: If the points plotted on the scatter diagram lie on a straight line and have a positive slope, then it can be said that the correlation is perfect and positive. However, if the points plotted lie on a straight line and have a negative slope, then it can be said that the correlation is perfect and negative.

Example:

Draw a Scatter Diagram for the following data and state the type of correlation between the given two variables X and Y.

Information Table

Solution:

We will draw the scatter diagram by plotting the values of Series X on the X-axis and values of Series y on the Y-axis (10, 80), (20, 160),………(60, 480).

Scatter Diagram

We can see that all the points of the given two variables X and Y are plotted on a positively sloping straight line, which means that there is a Positive Correlation between the values of Series X and Y.

Merits of Scatter Diagram

1. Simplicity: Scatter Diagram is a simple and non-mathematical method to study correlation between two variables.

2. First Step: It is the first step of investigating the relationship between two variables.

3. Easily Understandable: One can easily understand and interpret scatter diagrams. Besides, only at a single glance at the diagram, one can easily tell the presence or absence of correlation.

4. Not Affected by Extreme Items: The size of extreme values does not affect the scatter diagram. It is a quality which is not present in most mathematical methods.

Demerits of Scatter Diagram

1. Rough Measure: Scatter diagram only gives a rough idea of the degree and nature of correlation between the given two variables. Therefore, it is only a qualitative expression rather than a quantitative expression.

2. Non-mathematical Method: Like other methods of correlation, Scatter Diagram Method does not indicate the exact numerical value of correlation. 

3. Unsuitable for Large Observations: If there are more than two variables, it becomes difficult to draw a scatter diagram.

2. Karl Pearson’s Coefficient of Correlation:

Karl Pearson’s coefficient of correlation is denoted by r and can be used to measure correlation in case of both individual series as well as grouped data. Correlation Meaning Definitions Types Methods

The first person to give a mathematical formula for the measurement of the degree of relationship between two variables in 1890 was Karl Pearson. Karl Pearson’s Coefficient of Correlation is also known as Product Moment Correlation or Simple Correlation Coefficient. This method of measuring the coefficient of correlation is the most popular and is widely used. It is denoted by ‘r’, where r is a pure number which means that r has no unit. 

According to Karl Pearson, “Coefficient of Correlation is calculated by dividing the sum of products of deviations from their respective means by their number of pairs and their standard deviations.”

Karl~Pearson's~Coefficient~of~Correlation(r)=\frac{Sum~of~Products~of~Deviations~from~their~respective~means}{Number~of~Pairs\times{Standard~Deviations~of~both~Series}}

Or

r=\frac{\sum{xy}}{N\times{\sigma_x}\times{\sigma_y}}

Where,

N = Number of Pair of Observations

x = Deviation of X series from Mean (X-\bar{X})

y = Deviation of Y series from Mean (Y-\bar{Y})

\sigma_x  = Standard Deviation of X series (\sqrt{\frac{\sum{x^2}}{N}})

\sigma_y  = Standard Deviation of Y series (\sqrt{\frac{\sum{y^2}}{N}})

r = Coefficient of Correlation

Table of Content

  • Methods of Calculating Karl Pearson’s Coefficient of Correlation
  • 1. Actual Mean Method
  • 2. Direct Method
  • 3. Short-Cut Method/Assumed Mean Method
  • 4. Step Deviation Method
  • Change of Scale and Origin

Methods of Calculating Karl Pearson’s Coefficient of Correlation

  1. Actual Mean Method
  2. Direct Method
  3. Short-Cut Method/Assumed Mean Method/Indirect Method
  4. Step-Deviation Method

1. Actual Mean Method

The steps involved in the calculation of coefficient of correlation by using Actual Mean Method are:

  1. The first step is to calculate the mean of the given two series (say X and Y).
  2. Now, take the deviation of X series from \bar{X}  and denote the deviations by x.
  3. Square the deviations of x and obtain the total; i.e., \sum{x^2}  
  4. Take the deviation of Y series from \bar{Y}  and denote the deviations by y.
  5. Square the deviations of y and obtain the total; i.e., \sum{y^2}  
  6. Multiply the respective deviations of Series X and Y and obtain the total; i.e., \sum{xy} .
  7. Now, use the following formula to determine the Coefficient of Correlation:

r=\frac{\sum{xy}}{\sqrt{\sum{x^2}\times{\sum{y^2}}}}

Example:

Use Actual Mean Method and determine the coefficient of correlation for the following data:

Data Table

Solution:

Coefficient of Correlation

\bar{X}=\frac{\sum{X}}{N}=\frac{168}{7}=24

\bar{Y}=\frac{\sum{Y}}{N}=\frac{105}{7}=15

r=\frac{\sum{xy}}{\sqrt{\sum{x^2}\times{\sum{y^2}}}}

∑xy = 336, ∑x2 = 448, ∑y2 = 252

r=\frac{336}{\sqrt{448\times252}}=\frac{336}{\sqrt{1,12,896}}=\frac{336}{336}=1

Coefficient of Correlation = 1

It means that there is a perfect positive correlation between the values of Series X and Series Y.

2. Direct Method

The steps involved in the calculation of coefficient of correlation by using Direct Method are:

  1. The first step is to calculate the sum of Series X (∑X).
  2. Now, calculate the sum of Series Y (∑Y).
  3. Square the values of X Series and calculate their total; i.e., ∑X2.
  4. Square the values of Y Series and calculate their total; i.e., ∑Y2.
  5. Multiply the values of Series X and Y and calculate their total; i.e., ∑XY.
  6. Now, use the following formula to determine Coefficient of Correlation:

r=\frac{N\sum{XY}-\sum{X}.\sum{Y}}{\sqrt{N\sum{X^2}-(\sum{X})^2}{\sqrt{N\sum{Y^2}-(\sum{Y})^2}}}

Example:

Use Direct Method and determine the coefficient of correlation for the following data:

Data Table

Solution:

Coefficient of Correlation

r=\frac{N\sum{XY}-\sum{X}.\sum{Y}}{\sqrt{N\sum{X^2}-(\sum{X})^2}{\sqrt{N\sum{Y^2}-(\sum{Y})^2}}}

=\frac{(7\times2,856)-(168\times105)}{\sqrt{(7\times4,480)-(168)^2}\times{\sqrt{(7\times1,827)-(105)^2}}}

=\frac{19,992-17,640}{\sqrt{31,360-28,224}\times{\sqrt{12,789-11,025}}}

=\frac{2,352}{\sqrt{3,136}\times{\sqrt{1,764}}}=\frac{2,352}{56\times42}

=\frac{2,352}{2,352}=1

Coefficient of Correlation = 1

It means that there is a perfect positive correlation between the values of Series X and Series Y.

3. Short-Cut Method/Assumed Mean Method

Actual Mean can sometimes come in fractions which can make the calculation of standard deviation complicated and difficult. In those cases, it is suggested to use Short-Cut Method to simplify the calculations. The steps involved in the calculation of coefficient of correlation by using Assumed Mean Method are:

  1. First of all, take the deviations of X Series from the assumed mean and denote the values by dx. Calculate their total; i.e., ∑dx.
  2. Now, square the deviations of X series and calculate their total; i.e., ∑dx2.
  3. Take the deviations of Y Series from the assumed mean and denote the values by dy. Calculate their total; i.e., ∑dy.
  4. Square the deviations of Y series and calculate their total; i.e., ∑dy2.
  5. Multiply dx and dy and calculate their total; i.e., ∑dxdy.
  6. Now, use the following formula to determine Coefficient of Correlation:

r=\frac{N\sum{dxdy}-\sum{dx}.\sum{dy}}{\sqrt{N\sum{dx^2}-(\sum{dx})^2}{\sqrt{N\sum{dy^2}-(\sum{dy})^2}}}

Where,

N = Number of pair of observations

∑dx = Sum of deviations of X values from assumed mean

∑dy = Sum of deviations of Y values from assumed mean

∑dx2 = Sum of squared deviations of X values from assumed mean

∑dy2 = Sum of squared deviations of Y values from assumed mean

∑dxdy = Sum of the products of deviations dx and dy

Example:

Use Assumed Mean Method and determine the coefficient of correlation for the following data:

Data Table

Solution:

Coefficient of Correlation

r=\frac{N\sum{dxdy}-\sum{dx}.\sum{dy}}{\sqrt{N\sum{dx^2}-(\sum{dx})^2}{\sqrt{N\sum{dy^2}-(\sum{dy})^2}}}

=\frac{(7\times420)-(28\times21)}{\sqrt{(7\times560)-(28)^2}\times{\sqrt{(7\times315)-(21)^2}}}

=\frac{2,940-588}{\sqrt{3,920-784}\times{\sqrt{2,205-441}}}

=\frac{2,352}{\sqrt{3,136}\times{\sqrt{1,764}}}=\frac{2,352}{56\times42}

=\frac{2,352}{2,352}=1

Coefficient of Correlation = 1

It means that there is perfect positive correlation between the values of Series X and Series Y.

4. Step Deviation Method

This method simplifies the calculation of coefficient of correlation as the deviations are taken from assumed means and are divided by a common factor. The steps involved in the calculation of coefficient of correlation by using Step Deviation Method are:

  1. First of all, take the deviations of Series X from the assumed mean and divide them by Common Factor (C) to determine step deviation (dx^\prime) . Calculate the total of step deviations; i.e., \sum{dx^\prime}
  2. Take the deviations of Series Y from the assumed mean and divide them by Common Factor (C) to determine step deviation (dy^\prime) . Calculate the total of step deviations; i.e., \sum{dy^\prime}
  3. Square the step deviation of Series X and determine their total; i.e., \sum{dx^\prime{^2}}
  4. Square the step deviation of Series Y and determine their total; i.e., \sum{dy^\prime{^2}}
  5. Multiply (dx^\prime)  and (dy^\prime) , and determine their total; i.e., \sum{dx^\prime{dy^\prime}}
  6. Now, use the following formula to determine Coefficient of Correlation:

r=\frac{N\sum{dx^\prime{dy^\prime}}-\sum{dx^\prime}.\sum{dy^\prime}}{\sqrt{N\sum{dx^\prime{^2}}-(\sum{dx^\prime})^2}{\sqrt{N\sum{dy^\prime{^2}}-(\sum{dy^\prime})^2}}}

Where,

N = Number of pair of observations

\sum{dx^\prime}  = Sum of deviations of X values from assumed mean

\sum{dy^\prime}  = Sum of deviations of Y values from assumed mean

\sum{dx^\prime{^2}}  = Sum of squared deviations of X values from assumed mean

\sum{dy^\prime{^2}}  = Sum of squared deviations of Y values from assumed mean

\sum{dx^\prime{dy^\prime}}  = Sum of the products of deviations (dx^\prime)  and (dy^\prime)

Example:

Use Step Deviation Method and determine the coefficient of correlation for the following data:

Data Table

Solution:

Coefficient of Correlation under Step Deviation Method

r=\frac{N\sum{dx^\prime{dy^\prime}}-\sum{dx^\prime}.\sum{dy^\prime}}{\sqrt{N\sum{dx^\prime{^2}}-(\sum{dx^\prime})^2}{\sqrt{N\sum{dy^\prime{^2}}-(\sum{dy^\prime})^2}}}

=\frac{(7\times35)-(7\times7)}{\sqrt{(7\times35)-(7)^2}\times{\sqrt{(7\times35)-(7)^2}}}

=\frac{245-49}{\sqrt{245-49}\times{\sqrt{245-49}}}

=\frac{196}{\sqrt{196}\times{\sqrt{196}}}=\frac{196}{14\times14}

=\frac{196}{196}=1

Coefficient of Correlation = 1

It means that there is a perfect positive correlation between the values of Series X and Series Y.

Change of Scale and Origin

Coefficient of Correlation does not depend upon the change of scale and origin. 

  • Change of Origin: If a constant is added or subtracted to the values then it will not have any effect on the value of correlation coefficient.
  • Change of Scale: Similarly, if a constant is multiplied or divided by the values, then it will not have any effect on the value of correlation coefficient.

Example:

Find the coefficient of correlation from the following figures:

Data Table

Solution:

As the coefficient of correlation is not affected by the change in scale and origin of the variables, we will multiply the X Series by 10 and divide the Y series by 100.

Coefficient of Correlation

r=\frac{N\sum{dxdy}-\sum{dx}.\sum{dy}}{\sqrt{N\sum{dx^2}-(\sum{dx})^2}{\sqrt{N\sum{dy^2}-(\sum{dy})^2}}}

=\frac{(8\times156)-[(-24)\times(-4)]}{\sqrt{(8\times1,584)-(-24)^2}\times{\sqrt{(8\times44)-(-4)^2}}}

=\frac{1,248-96}{\sqrt{12,672-576}\times{\sqrt{352-16}}}

=\frac{1,152}{\sqrt{12,096}\times{\sqrt{336}}}=\frac{1,152}{110\times18.3}

=\frac{1,152}{2,013}=0.57

Coefficient of Correlation = 0.57

It means that there is a moderate degree of positive correlation between variables X and Y.

Merits of Karl Pearson’s co-efficient of Correlation Method:

1. The Karl Pearson’s coefficient of correlation gives the exact measure of correlation between variables.

2. It gives both the direction and the degree of relationship between variables.

Demerits of Karl Pearson’s co-efficient of Correlation Method:

1. It always assumes a linear relationship between variables.

2. The value of the coefficient is affected by the presence of extreme values.

3. It takes time to calculate the correlation coefficient using this method and it is a complicated method as compared to other measures of correlation. 

3. Spearman’s Rank Correlation Coefficient:

The Karl Pearson’s coefficient of correlation is computed based on the assumption that the observations are normally distributed. However, when the distribution of the observations is not known, then one cannot use the previously mentioned methods of calculating correlation. Also, Karl Pearson’s coefficient of correlation is unsuitable to study the correlation between two qualitative variables, such as honesty and beauty. Correlation Meaning Definitions Types Methods

In all such cases, Spearman’s rank correlation coefficient can be applied to study the relationship between two variables. In this method, the variables need to be assigned ranks based on their size from the smallest to the largest or from the largest to the smallest.

This method is named after the British Psychologist Charles Edward Spearman, who developed it in 1904.

Methods of correlation – Spearman’s rank correlation coefficient is computed in the following manner:

1. When Ranks are given:

When the ranks have already been assigned to the items, the following steps are to be used in calculating correlation:

(i) Calculate the difference (D) between two ranks, i.e. Rx – Ry.

(ii) The differences have to be squared (D2) and their sum is to be taken as ZD2.

(iii)Then the following formula is to be used to calculate the correlation coefficient:

If the data are in ordinal scale then Spearman’s rank correlation coefficient is used. It is denoted by the Greek letter ρ (rho).

Spearman’s correlation can be calculated for the subjectivity data also, like competition scores. The data can be ranked from low to high or high to low by assigning ranks.

Spearman’s rank correlation coefficient is given by the formula

where Di = R1i – R2i

R1i = rank of i in the first set of data

R2i = rank of i in the second set of data and

n = number of pairs of observations

Example 4.3

Two referees in a flower beauty competition rank the 10 types of flowers as follows:

Use the rank correlation coefficient and find out what degree of agreement is between the referees.

Solution:

Interpretation: The degree of agreement between the referees ‘A’ and ‘B’ is 0.636 and they have  “strong agreement” in evaluating the competitors.

2. When Ranks are Not Given:

When the ranks are not already associated with the items and rather the marks or the values are assigned to each item, then the ranks have to be given to each item based on the values or the marks attached to them.

The following steps are to be followed when ranks are not given:

(i) First the rank is to be assigned to each item in the distribution. The variables can be assigned ranks on the basis of their size from smallest to largest or from largest to smallest.

(ii) Calculate the difference (D) of the two ranks, i.e. Rx – Ry.

(iii) The differences have to be squared (D2) and their sum is to be taken as ΣD2.

(iv)Then the following formula is to be used:

Calculate the Spearman’s rank correlation coefficient for the following data.

Solution:

Interpretation: This perfect negative rank correlation (- 1) indicates that scorings in the subjects, totally disagree. Students who are best in Tamil are weakest in English subjects and vice-versa.

3. When Ranks are Equal:

When there are equal ranks, for instance, when there are two 3rd ranks, then they are given the rank (3+4)/2 = 3.5 and if there are three 3rd ranks, then it becomes (3+4+5)/3=4.

This adjustment is incorporated in the formula as follows:

Repeated ranks

When two or more items have equal values (i.e., a tie) it is difficult to give ranks to them. In such cases the items are given the average of the ranks they would have received. For example, if two individuals are placed in the 8th place, they are given the rank [8+9] / 2 = 8.5 each, which is common rank to be assigned and the next will be 10; and if three ranked equal at the 8th place, they are given the rank [8 + 9 +10] /3  = 9 which is the common rank to be assigned to each; and the next rank will be 11.

In this case, a different formula is used when there is more than one item having the same value.

where mi is the number of repetitions of ith rank

Where, D = Difference of rank in the two series

N = Total number of pairs

m = Number of times each rank repeats

Example 4.6

Compute the rank correlation coefficient for the following data of the marks obtained by 8 students in the Commerce and Mathematics.

Solution:

Repetitions of ranks

In Commerce (X), 20 is repeated two times corresponding to ranks 3 and 4. Therefore, 3.5 is assigned for rank 2 and 3 with m1=2.

In Mathematics (Y), 30 is repeated three times corresponding to ranks 3, 4 and 5. Therefore, 4 is assigned for ranks 3,4 and 5 with m2=3.

Therefore,

Interpretation: Marks in Commerce and Mathematics are uncorrelated

Merits of Spearman’s Rank Correlation Coefficient:

1. It is simple to understand.

2. It is easy to calculate as compared to the Karl Pearson’s correlation method.

3. It can be easily applied when the data is qualitative in nature. For example, the level of satisfaction derived by the two consumers from different products can easily be ranked and degree of correlation can be computed.

4. This method can also be applied when the data is not in the form of ranks. The actual data can be converted to ranks in such cases.

Demerits of Spearman’s Rank Correlation Coefficient:

1. This method cannot be applied when the data is in the form of a grouped frequency distribution.

2. The calculation of Spearman’s rank correlation coefficient becomes time-consuming when the data is very large and when ranks are not given.

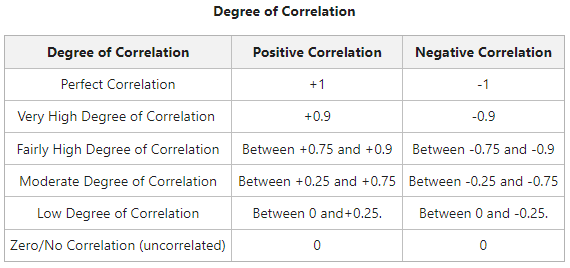
Degrees of Correlation

Within these limits, the value or degrees of correlation can be interpreted as:

Degree of Correlation

Properties of Coefficient of Correlation

The following are the main properties of correlation. Properties of Correlation

1. Coefficient of Correlation lies between -1 and +1:

The coefficient of correlation cannot take value less than -1 or more than one +1. Symbolically,

-1<=r<= + 1 or | r | <1.

2. Coefficients of Correlation are independent of Change of Origin:

This property reveals that if we subtract any constant from all the values of X and Y, it will not affect the coefficient of correlation.

3. Coefficients of Correlation possess the property of symmetry: Rxy=Ryx

4. Coefficient of Correlation is independent of Change of Scale:

This property reveals that if we divide or multiply all the values of X and Y, it will not affect the coefficient of correlation.

5. Co-efficient of correlation measures only the linear correlation between X and Y.

6. If two variables X and Y are independent, the coefficient of correlation between them will be zero.

 

Complete Business Statistics eBook – Download Now

 

Discover more from Easy Notes 4U Academy

Subscribe to get the latest posts sent to your email.

Written by 

Dr. Gaurav has a doctorate in management, a NET & JRF in commerce and management, an MBA, and a M.COM. Gaining a satisfaction career of more than 10 years in research and Teaching as an Associate professor. He published more than 20 textbooks and 15 research papers.

Visit Website

Other posts by author

Leave a Reply